
ОГЭ 9 класс по математике с ответами
ОГЭ 9 класс по математике.
Часть 1 ОГЭ 9 класс по математике
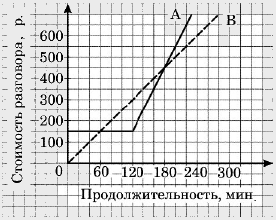
1. Площадь территории Испании составляет 506 тыс. км2. Как эта величина записывается в стандартном виде? Из 59 девятиклассников школы 22 человека приняли участие в городских спортивных соревнованиях. Сколько приблизительно процентов девятиклассников приняли участие в соревнованиях? Числа a и b отмечены точками на координатной прямой. Расположите в порядке возрастания числа Найдите значение выражения Из формулы периода обращения Какое из приведённых ниже выражений тождественно равно произведению (x−4)(x−2)? Представьте выражение Какое из данных выражений не равно выражению Решите уравнение x2 +7x−18=0. Гипербола, изображённая на рисунке, задаётся уравнением Прочитайте задачу: Решите неравенство 20−3(x+5)<1−7x. При каких значениях х верно неравенство x2 +2x−3<0? Из арифметических прогрессий, заданных формулой n-го члена, График какой из перечисленных ниже функций изображён на рисунке? Компания предлагает на выбор два разных тарифа для оплаты телефонных разговоров: тариф А и тариф В. Для каждого тарифа зависимость стоимости разговора от его продолжительности изображена графически. На сколько минут хватит 550 р., если используется тариф В? На каждые 1000 электрических лампочек приходится 5 бракованных. Какова вероятность купить исправную лампочку? Записан рост (в сантиметрах) пяти учащихся: 158, 166, 134, 130, 132. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
1) 5,06 · 102 км2
2) 5,06 · 103 км2
3) 5,06 · 104 км2
4) 5,06 · 105 км2
2.
1) 0,37% 2) 27% 3) 37% 4) 2,7%


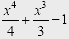
при x = 1.
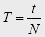
выразите время вращения t.
1) (x−4)(2−x)
2) −(x−4)(2−x)
3) (4−x)(x−2)
4) −(4−x)(2−x)
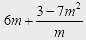
в виде дроби.
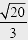

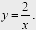
Используя рисунок, установите соответствие между системами уравнений и утверждениями.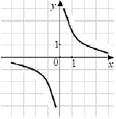
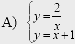 1) система имеет одно решение
1) система имеет одно решение 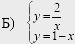 2) система имеет два решения
2) система имеет два решения 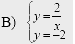 3) система не имеет решений.
3) система не имеет решений.
11.
«Фотография имеет форму прямоугольника со сторонами 10 см и 15 см. Её наклеили на белую бумагу так, что вокруг фотографии получилась белая окантовка одинаковой ширины. Площадь, которую занимает фотография с окантовкой, равна 500 см2. Какова ширина окантовки?»
Пусть ширина окантовки равна х см. Какое уравнение соответствует условию задачи?
1) (10+2x)(15+2x)=500
2) (10+x)(15+x)=500
3) 10⋅15+(10x+15x)⋅2=500
4) (10+2x)(15+x)=500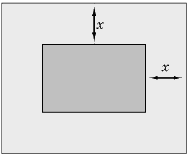
12.
выберите ту, для которой выполняется условие a25<0.
1) an = 2n
2) an = −2n+50
3) an = −2n+100
4) an = 2n−100
1) y=x2 +4
2) y=x2 +4x
3) y= −x2 − 4x
4) y= −x2 − 4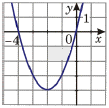
16.
Часть 2 ОГЭ 9 класс по математике:
19. Решите уравнение x3−6x2−4x+24=0. Решите неравенство В геометрической прогрессии сумма первого и второго членов равна 108, а сумма второго и третьего членов равна 135. Найдите первые три члена этой прогрессии. Прямая y=2x+b касается окружности x2+y2=5 в точке с положительной абсциссой. Определите координаты точки касания. Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?
20.
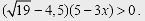
21.
22.
23.
Ответы к заданиям части 1 ОГЭ 9 математика:
№ задания Ответ
1 - 4
2 - 3
3 - 1
4 - 5/12
5 - t=TN
6 - 2
7 - 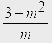
8 - 4
9 - x1 = 2, x2 = − 9
10 - 231
11 - 1
12 - x < −1
13 - − 3 < x < 1 или (−3; 1)
14 - 4
15 - 2
16 - На 220 мин.
17 - 0, 995
18 - На 10
Решение и ответы к заданиям части 2 ОГЭ 9 математика:
19. Решите уравнение x3 − 6x2 − 4x + 24 = 0. Ответ: –2; 2; 6. Решите неравенство В геометрической прогрессии сумма первого и второго членов равна 108, а сумма второго и третьего членов равна 135. Ответ: 48, 60, 75. Прямая y=2x+b касается окружности x2+y2=5 в точке с положительной абсциссой. Ответ:(2; –1). Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки? Ответ: плот пройдет 2/5 всего пути.
Решение. Разложим на множители левую часть уравнения.
Получим: x2(x−6)−4(x−6)=0, (x−6)(x2−4)=0, x −6 = 0 или
x2 −4=0.
Значит, уравнение имеет корни: –2; 2; 6.
20.
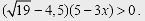
21.
Найдите первые три члена этой прогрессии.
22.
Определите координаты точки касания.
Решение.
1) Найдем значения b, при которых система

имеет единственное решение. Выполнив подстановку, получим уравнение x2 + (2x + b)2 = 5,
т.е. 5x2 + 4xb + b2 − 5 = 0.
2) Полученное уравнение имеет единственное решение, когда его дискриминант равен нулю.
Имеем: D1 = 4b2 − 5(b2 − 5) = 25 − b2. Решив уравнение 25 − b2 = 0, получим b = ±5.
3) Таким образом, получили уравнения двух прямых, касающихся окружности: y=2x+5 и y=2x−5.
Найдем абсциссы точек касания, подставив найденные значения b в уравнение
5x2 + 4xb + b2 − 5 = 0:
при b = 5 получим уравнение x2 + 4x + 4 = 0, откуда х = –2; этот корень не удовлетворяет условию задачи;
при b = –5 получим уравнение x2 − 4x + 4 = 0, откуда х = 2.
Найдем соответствующее значение у: y = 2x − 5 = 2 · 2−5 = −1.
Координаты точки касания (2; –1).
23.
Решение.
Пусть скорость течения реки (и плота) х км/ч. Тогда скорость катера против течения равна 4х – х = 3х км/ч, а по течению 4х + х = 5х км/ч. Следовательно, скорость катера против течения в 3 раза больше скорости плота, а по течению – в 5 раз больше скорости плота. Если плот до встречи проплыл S км, то катер – в 3 раза больше, т.е. 3S км. После встречи катер пройдет 3S км, а плот – в 5 раз меньше, т.е. 3S⁄5 км. Всего плот пройдет S + 3S⁄5 = 8S⁄5.
Отношение пройденного плотом пути ко всему пути равно
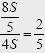
Другое возможное решение.
Пусть скорость течения реки (и плота) х км/ч.
Тогда скорость катера против течения равна 4х – х = 3х км/ч, а по течению 4х + х = 5х км/ч.
Скорость сближения катера и плота равна х + 3х = 4х км/ч. Встреча произошла через AB/4x ч. За это время плот проплыл x · AB/4x = AB/4 км, а катер – 3AB/4 км.
Обратный путь катер пройдет за
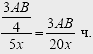
Плот за это время проплывет расстояние, равное x · 3AB/20x = 3AB/20 км, а всего он проплывет AB/4 + 3AB/20 = 2/5 AB км.